An adjustment to Newton’s gravity?

For 85 years, astronomers have noted that there is more gravity than they can account for in the galaxies that they see, in clusters of galaxies, and in the dynamics of the whole universe. What is the invisible source of that extra attraction? Last week there was striking new evidence for a dark horse theory — Maybe there is no missing matter, but instead gravity doesn’t work as Newton taught us that it does.

---

Missing mass

Starting in the 1930s, astronomers noticed that gravity was pulling harder than physics could account for. We think we know the masses of stars, and we can measure how fast they are moving in orbit using the Doppler effect (“redshift”). We can compare this with the predicted orbital speed from Newton’s equations of motion.

Galaxies failed this simple test. The stars toward the out edges of galaxies were moving too fast, as if there were more mass in the galaxy than the stars could account for, or else gravity were stronger than theory predicts.

Of course, astronomical observations have a lot of uncertainty. The discrepancy only became a concern because the missing mass was a great deal larger than the star mass. Gravity appeared to be more than ten times stronger than astronomers could account for. And as observations got better and uncertainty narrowed, the problem only became more pronounced.

When astronomers started looking at clusters of galaxies, there was even more missing mass, and in the Universe as a whole there is more yet.

Today, the missing mass is considered one of the greatest unsolved problems in astronomy. What is it made of and why can’t we see it? There are good arguments that it can’t be stars or planets or dust or, indeed, anything made of ordinary atoms. Neutrinos are particles that can be seen in accelerators that are very hard to detect, and there are good reasons to think that the missing mass is not neutrinos. An intense hunt is ongoing to try to detect “dark matter”, and so far it has failed.

Astronomers realize, of course, that it isn’t good science to invent some new kind of invisible, undetectable matter just to account for the extra gravity, but that’s where we have been stuck for the last 25 years.

Modified Newtonian Dynamics

Maybe there isn’t any missing matter, but gravity doesn’t work quite the way that we expect. Newton gave us the law of gravitation 300 years ago, and it has held up pretty well. Gravitational force is proportional to the mass of a gravitating body, and decreases with the square of the distance.

Einstein’s general relativity is a well-accepted modification of Newtonian gravity that becomes significant only when gravity is very strong, close to a black hole or a neutron star.

In 1983, Israeli physicist Mordehai Milgrom proposed that Newtonian gravity might also need modification in situations where gravity is very weak. To account for the stars and galaxies that are moving too fast for their orbits, he proposed to modify Newton’s law so that it gradually changed from the standard 1/R² to 1/R. He characterized the regime in which this transition takes place, and he found he was able to account pretty well for the orbital speeds if the transition happens when acceleration is less than 10^-10 m/sec², which is about a hundred billion times weaker than the gravity that you and I are swimming in.

Physicists have embraced Einstein’s modification of Newton, but we have balked at Milgrom’s proposal. The reason is purely aesthetic. Einstein framed his general relativity in terms of elegant geometrical equations. The structure of the equations was changed profoundly, but no arbitrary parameters were added. Einstein’s equations become Newton’s equations except when gravity is very, very strong; so astronomers could keep all the results that worked well. Milgrom’s paradigm, on the other hand, is empirical. It’s the kind of exercise you do when you have experimental points and you look for a formula for a curve that passes through those points. Engineers do this all the time, but physicists judge it to be inelegant.

The upshot is that if you look in the astronomy journals, you’ll find a hundred articles that propose resolution to “what is dark matter made of?” for every one that discusses MOND. MOND=Modified Newtonian Dynamics is the standard acronym for Milgrom’s theory.

Two intuitive properties of gravity that MOND gives up

First, Newtonian gravity is linear. For example, a mass A can create a gravitational field at a certain position, and another mass B effects the gravitational field at that same spot. When both A and B are present, you can just add the gravitational fields from each one separately. Electromagnetism and even the nuclear strong and weak forces have this property, but MOND does not. This will play tricks with your intuition if you try to imagine ways to test MOND. A hint is in the fact that MOND is “Modified Newtonian Dynamics”, not MONG (modified Newtonian gravity). You might think about it as a way that matter responds to gravitational forces in particular that is different from the way matter responds to other forces, and it is not at all clear that the theory can be fit into the rest of physics in a self-consistent way. People have thought deeply about this problem and they are convinced that it can be a logically coherent theory, but I have not yet understood the deeper issues.

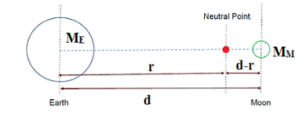
To illustrate how hard it is to think about Milgrom’s theory, imagine traveling further and further from the earth, watching gravity get weaker and weaker. Then you get to a place where gravity is weaker than 10^-10 m/sec² and the gravity starts to change more slowly. So far so good. But now put the moon in the picture. As you leave the pull of the earth, the field may still be far stronger than the 10^-10 m/sec² range where you expect trouble. But there is a place where the earth pulls to the left and the moon pulls to the right, and the net field is very small as a result. What does MOND predict will happen here? Does gravity start to fall off as 1/R₁ from the earth and also increase as 1/R₂ as you approach closer to the moon? MOND proponents have had to think about such strange questions, which don’t arise in Newtonian or Einsteinian gravity.

Second is the “equivalence principle”, which is an unspoken property of Newtonian gravity and a postulate at the heart of Einsteinian gravity. The equivalence principle says simply that you can’t tell the difference between an accelerating frame of reference and a gravitational field. If you’re in the orbiting International Space Station, you’re in the earth’s gravitational field, but you don’t feel it because you and the station are moving (accelerating) together. You experience zero gravity from your perspective. From an outsider’s perspective, the earth’s gravitational field is being counterbalanced exactly by the motion of the Space Station. In MOND, the equivalence principle is only approximately true.

Newton’s equations are simple and elegant. Einstein’s equations are yet simpler and more elegant, though they require a great deal of mathematical sophistication to appreciate their simplicity. MOND is not an elegant or “beautiful” theory. Sabine Hossenfelder’s message is that we need to let that go and think of every theory as a model rather than a true picture of “physical reality”. We must put our aesthetic response aside and choose the model that best fits the data. This appears at first blush to be sound science, but as we think more deeply, we discover that Occam’s Razor is central to scientific thinking, and that scientists have been seeking beauty and elegance since the time of Aristotle.

Perhaps, science would be more scientific if we gave up our quest for Grand Unified Theories and instead focused on creating diverse mathematical models that work well within their particular range of validity. For the scientific community, this would be a major cultural shift. We are not ready to give up the Zeroth Law of Science.

Sabine Hossenfelder

Dr Hossenfelder is a particle physicist who has a popular podcast. She has taken a stand that physicists pay too much attention to elegance in a theory, and not enough attention to the simplest explanation for the facts at hand. She announced a few years ago that she’s leaning toward some version of the MOND theory.

One of the mysterious generalities that come out of observational astronomy is that, after you leave the central core of each galaxy, the stars seem to be going around the core at the same speed, regardless of how far they are from the core. That speed is proportional to the square root of the square root of the galaxy’s mass (v ~ M^¼). This is called the Tully-Fisher relation, observed but not explained, until MOND which was designed to be consistent with  exactly this observation.

Beyond this, MOND fits pretty well the speeds of galaxy clusters. Sometimes a nearby galaxy sits right on the line of sight of a brighter galaxy behind it, and the nearby bends the light from the further galaxy inward toward us, so that we see multiple images or a halo or both.

This is called gravitational lensing, and it is also observed to happen more strongly than the observed mass can explain. MOND does a pretty good job with this as well.

The largest scale anomalies are not solved by MOND. When cosmologists try to put together models of the Universe as a whole, the models don’t naturally produce galaxies early enough and they don’t accelerate their expansion as time goes on. Dark matter and dark energy in just the right amounts have been added to explain these things. This is another kind of ad hoc assumption, making the theory inelegant and aesthetically unappealing.

Last week

A Korean research group published a paper in Astrophysical Journal applying MOND in a regime where it had never been tested, and where dark matter would not be expected to contribute anything at all. MOND passed the test with flying colors.

Dark matter is expected to be important on large scales, while the modifications of Newton’s gravity in MOND happen wherever the field is weak, regardless of whether the scale is large or small. So the Korean group chose to study a system where gravity is weak but distances are not large. The system they chose was a class of “double stars” that are so far apart that you might not even recognize them as “double”, nevertheless they are bound together and orbiting around each other. They analyzed 26,000 “wide binaries” that are close enough to the earth that, with observations stretched out by a few years, you can actually see the stars moving across the sky. (Astronomers call this “proper motion”.)

It is the change in (proper) motion that constitutes acceleration. Detecting changes in proper motion would require at least three photographs of each star pair, and uncertainty is magnified in the process. So the Korean team chose a different path. Theirs was a modeling approach, very much in keeping with the spirit of MOND.

They measured the distribution of proper motions from 26,000 pairs of wide binaries. Then they compared the distribution to “expected” results when they randomly generated 26,000 of pairs of stars in a computer model. For masses of the stars and separation distances, they used the observed sample of 26,000. (Masses had to be inferred from luminosities of the stars, and this is a major subproject of their work.) For orientation of the system to our line of sight, they used random angles. For ellipticity of the orbits, they consulted databases of wide binaries.

The question they asked: If the computer models were built with standard Newtonian gravity, did the results match, statistically, the observed 26,000 proper motions? If not, would adding MOND improve the match?

The computer models could easily be tweaked with and without MOND of various strengths, and the best fit was with the same MOND parameters that had already been chosen because they work at larger scales (stars in galaxies and galaxies in clusters). This was the striking result that was framed as smoking gun evidence for MOND at a conservative and straight-laced science news site where I discovered it last week.

Of course, a pitfall of such a study would be that maybe the stars aren’t bound to each other at all. Then you would observe no acceleration, or random accelerations. But you would not expect to see what was actually observed, namely, stronger acceleration than Newton’s gravity could account for.

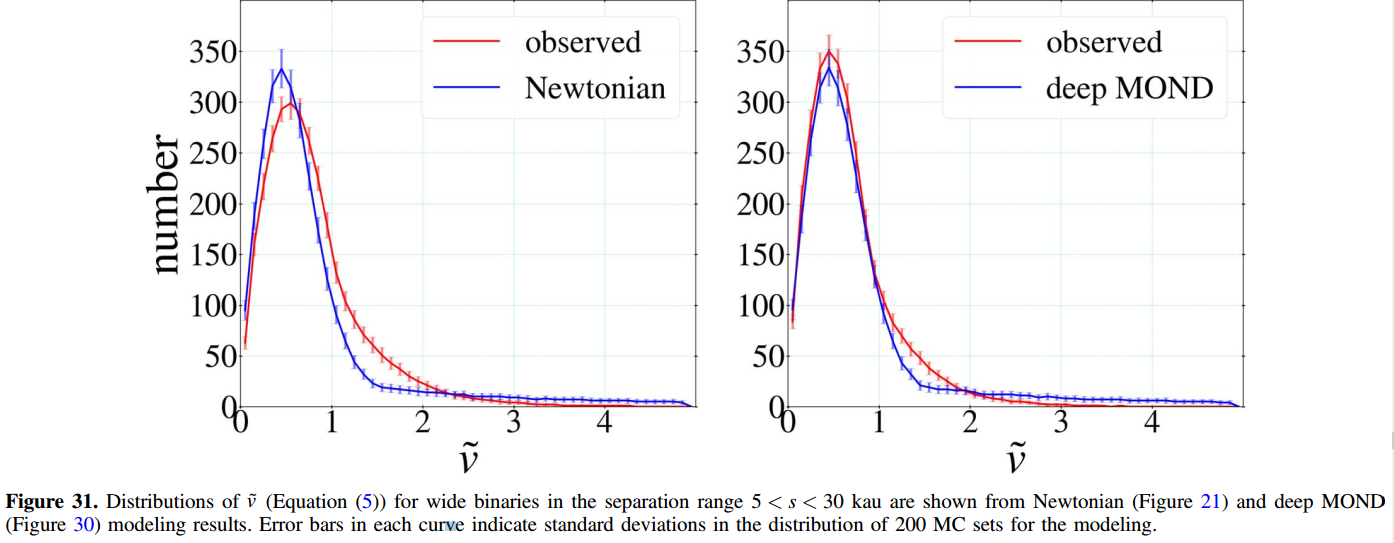
The first 30 figures in the paper establish and defend their methodology. Here, in figure 31, we finally see their result. The proper motions as simulated with MOND are a much better match to the 26,000 data points than the same simulation with Newtonian gravity.

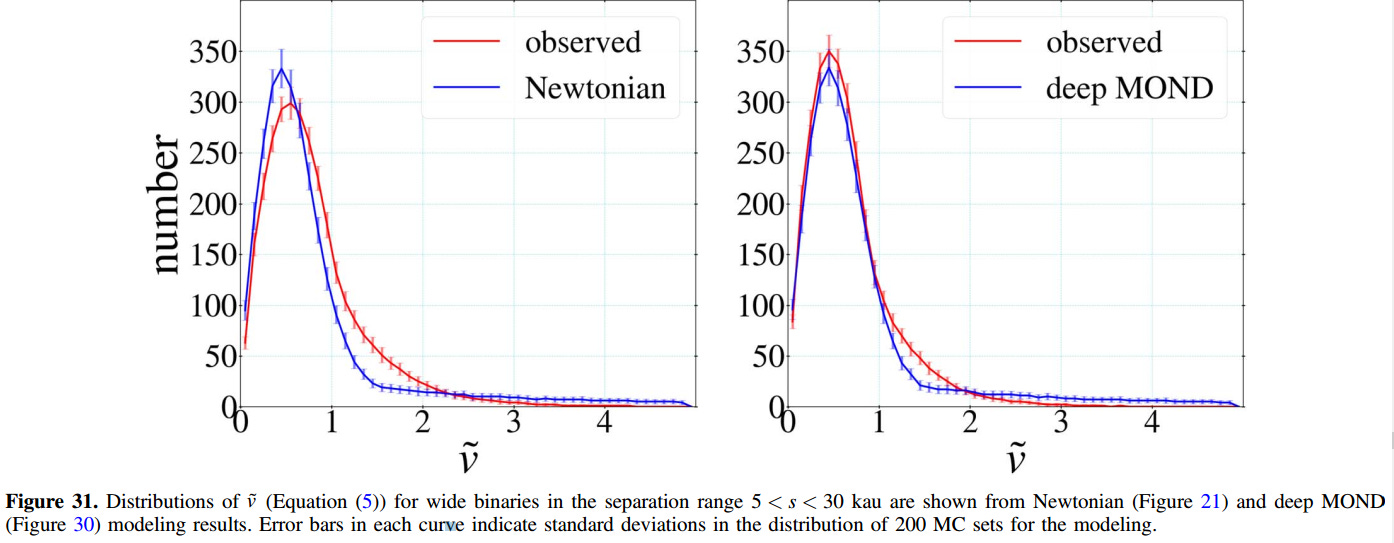
The strongest criticism of the study is that it was exceedingly complex, built on chains of reasoning, like a house of cards. This is, unfortunately, common in astrophysics. You can’t do experiments — you can only look at the sky, so we get embroiled in chains of reasoning that are fallible at every step. The description of their procedure is long and detailed. They convinced me that they did a conscientious job, using the information they had and making conservative assumptions where information was lacking.

• Why did they measure only proper motions (velocities) and not the difference in proper motions (accelerations) which would have been more directly comparable to MOND predictions?
• Why didn’t they incorporate redshifts, and changes in redshifts over time, which would have added information about acceleration along the line of sight to acceleration in the field of view?
• Why didn’t they subdivide their 26,000 sample according to the relative masses of the two stars, and compare this to corresponding subdivisions of their simulated data?

These are not criticisms, but suggestions for the next step.

Next stop, gravity in the lab

Before this work, MOND had been tested only on the scale of galaxies and galaxy clusters. The new study extended MOND to much smaller distances, and the model held up well. This is promising.

A next step would be to measure MOND in the laboratory. Tiny accelerations in the range of 10^-10 m/s² are actually measurable in the laboratory with laser interferometers, and this is already being done in Cavendish and Eötvös experiments.

In 1798, Henry Cavendish conducted the first modern experiments to measure gravity from human-scale objects directly. He used a torsion balance enclosed in a vacuum, a dumbbell hanging from a thin wire which twists left and right in response to tiny forces.

 

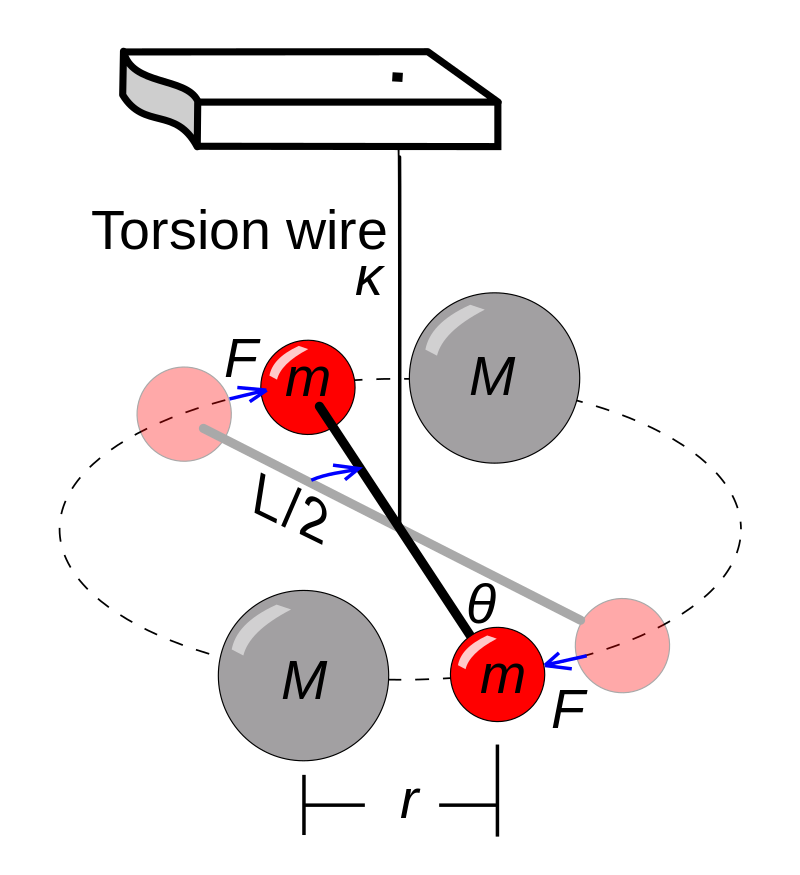
Loránd Eötvös was a pioneer in testing the equivalence of gravitational mass and inertial mass. We use the same m in the equation of motion F=ma and in GMm/R², but there is no logical reason why these two definitions of “mass” should coincide. Eötvös in the late 19th century used an apparatus similar to Cavendish but with different materials to test the equivalence.

Modern versions of these experiments have measured G, the universal constant that quantifies the strength of gravity, to a few parts per million, but different measurements vary by about 10 times the nominal error bars. Are the error bars just overly optimistic, or is there some physics that we haven’t yet accounted for?

To my knowledge, no one has yet suggested that the reason for these discrepancies between different experiments is that they are all analyzed in terms of Newtonian gravity (1/R²), even though the fields are weak enough that MOND might apply.

The next test of MOND should be in the laboratory, seeing if the tiny gravitational force from a lead bowling ball falls off as 1/R² or as 1/R or ??.  Repeating such measurements on the Space Station would also be revealing, because the principle of equivalence itself would be tested. “Gravity” itself isn’t weak in the space station, but gravity is canceled by an accelerated frame of reference. Einstein says the results should be the same, but Milgrom (MOND) is not so sure. Let’s find out.

What’s at stake

MOND is truly an ugly theory. It is not even clear if it can be made logically coherent. General Relativity is exactly the opposite — it is the most elegant mathematical framework in modern physics. If it turns out that MOND is better than GR at accounting for experimental results, the message will be that theoretical physics is overextended, that we should be less focused on finding the Theory of Everything and more satisfied with mathematical models that are found to be accurate within their limited domains.